オープンハウス ドキュメント(2024)
今回実装する処理
Day 1, 2は、以下を実装するコードを作成する。
- 人工データの生成
- 標準化
- 周波数解析
人工データの生成
[ ここをクリックして展開 / 折りたたみ ]
作成したプログラムが正しいかを確認するため、人工データを作成して検証する。
例を参考にコーディングしてください
実装の流れ
- 乱数の生成
- 複数の正弦波と乱数などを組み合わせた人工脳活動データを作成
- 複数試行を模擬した人工データを作成
準備 モジュール・ライブラリのインポート
Pythonでは以下のようなモジュール・ライブラリを利用する。
-
numpy
NumpyはPythonの主流なライブラリの一つで、ナムパイと読む。 Python単体で計算をおこなうより簡単に、かつ素早く計算を実行することが可能。
機械学習やデータ分析を中心に様々な分野で利用されている。
Numpy入門 -
matplotlib
matplotlibはnumpy配列を引数として、図を作成したりできる。
Matplotlib入門
# モジュール
import numpy as np
import matplotlib.pyplot as plt
1. 乱数の作成
人工データを作るときには試行のばらつきやノイズを乱数により作成する。
numpyのnp.randomを使い乱数を生成できる。生成されたデータはnumpyデータ型(クラス)のndarrayになる。ndarrayでは計算に有益なメソッドが多く定義されている(X.mean()など、numpy公式サイト methodsの説明)
# 乱数の生成
""" 乱数の生成 """
import matplotlib.pyplot as plt
import numpy as np
NUM_SAMPLES = 100 # 定数
t = np.arange(NUM_SAMPLES)
# 一様分布(0から1)
noise = np.random.rand(NUM_SAMPLES)
mean_noise = noise.mean()
std_noise = noise.std()
print("mean = ", mean_noise, "std = ", std_noise)
# 正規分布(平均0, 分散1)
noise_normal = np.random.randn(NUM_SAMPLES)
mean_noise_normal = noise_normal.mean()
std_noise_normal = noise_normal.std()
print("mean = ", mean_noise_normal, "std = ", std_noise_normal)
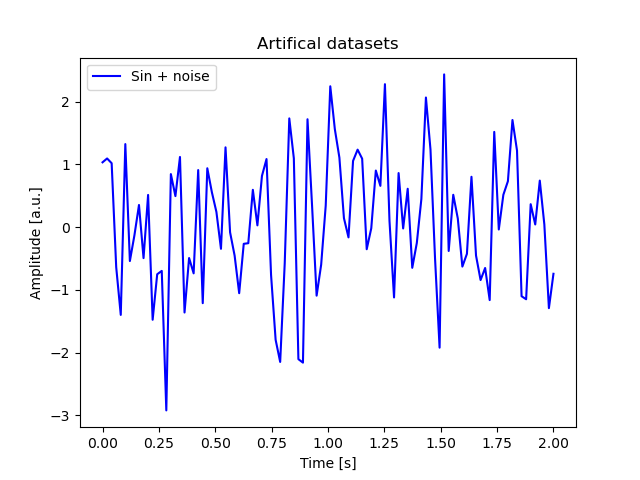
# グラフ表示(標準的な方法)
fig, ax = plt.subplots()
ax.set_title("Artifical datasets")
ax.set_xlabel("Time [s]")
ax.set_ylabel("Amplitude [a.u.]")
ax.plot(noise, label="noise")
ax.plot(noise_normal, label="normalized noise")
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles, labels)
plt.show()
2. 周期的な信号の生成
脳波などの生体信号はある周波数帯のデータが強くなったり、機能的な意味があったりする。これを模倣するため、周期的な人工データを生成する。
# -5 ~ 5 まで、100個のデータ(ndarray)を np.linespaceを使って作成
t2 = # 自分で作成, np.linespaceを使う
# Sin信号の生成
y_sin = # 自分で作成
3. 人工データの生成(1次元)
正弦波と乱数を組み合わせて人工時系列データを作成する。
- データの次元は1 x N_TIME の行列(N_TIME:データ数)
- サンプリング周波数なども自分で設定できるようにする
- 関数にするのが望ましい
# 例
""" 人工データの生成(1次元) """
import numpy as np
import matplotlib.pyplot as plt
# 関数化, defで関数を定義
def generate_artifical_timeseries(times, fs, freq):
"""
Generating artifical time series signals
y = generate_artifical_timeseries(times, fs, freq):
times: 時間(タイムスタンプ)の配列
fs: sampling frequency(サンプリング周波数)
freq: signal frequency(信号=人工データの周波数)
"""
omega = # 自分で作成、角周波数を定義
data = # 自分で作成、人工データを生成
noise = # 自分で作成、ノイズを生成
output = # 人工データ+ノイズを合成
return output
# サンプリング周波数、人工データの周波数、時間の長さを定義
FS = # [Hz]
F = # [Hz]
TIME = # [s] 秒
# np.arangeで時間データを作成
t = np.arange( )# 中身を自分で作成
# 信号生成
y = generate_artifical_timeseries(t, FS, F)
# 図で確認
fig, ax = plt.subplots()
ax.set_title("generated signal")
ax.set_xlabel("Time [s]")
ax.set_ylabel("Amplitude [a.u.]")
ax.plot(t, y)
plt.show()
標準化
[ ここをクリックして展開 / 折りたたみ ]
信号の分析において、測定した信号同士の特性を比較する手法がある。 しかし、データ毎に信号の平均や分散が異なることが原因で正しく評価できないことがある。 そこで、測定した信号の成分の平均μを0、標準偏差σを1とすることで比較を可能にする処理を標準化(Z-score化)と呼ぶ。 元信号を$x(t)$とするとき、以下の$Z$で表される。
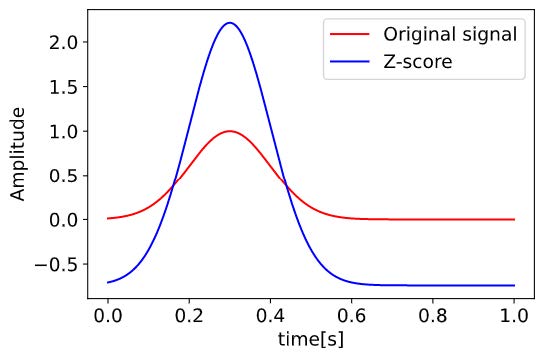
\[\begin{aligned} Z = \frac{x(t)-\mu}{\sigma} \end{aligned}\]下図に標準化の例を示す。 赤線が元信号で青線が標準化後の信号である。
標準化は単位・スケールの違う特徴量を連結して使用する際などに有効であるが、次元間のスケールが統一されている場合や使用する機械学習アルゴリズムによっては必ずしも必要ではない。
実装の流れ
- 疑似データの生成 上記図の例:
- 標準化処理 上に示した通り、平均と標準偏差を計算し、標準化を行う。
np.linespaceで時間軸を生成し、
$y = Aexp\left\lbrace-\frac{(x-\alpha)^2}{2\sigma^2}\right\rbrace$に当てはめて各パラメータに適当な値を入れた信号。
先に作った人工データやランダムデータでも可。
(例)
""" 正規化処理 """
import matplotlib.pyplot as plt
import numpy as np
# 関数の定義
def z_score(data):
"""
dataを入力して正規化したafter_dataを出力
"""
# (コーディング)
mean = # dataの平均値を求める
std = # dataの標準偏差を求める
z_scored = # z-scoreの算出
return z_scored
if __name__ == "__main__":
#(コーディング)
data = # データの作成(例:乱数、先に作った人工データを使用してもOK)
normalized_data = z_score(data)
# 比較のグラフ
fig, ax = plt.subplots()
ax.set_title(" ") # タイトル
ax.set_xlabel(" ") # x軸
ax.set_ylabel(" ") # y軸
ax.plot( ) # 元のデータを表示、labelはoriginalに設定
ax.plot( ) # 正規化したデータを表示、labelはz-scoredに設定
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles, labels) # legendの表示
plt.show()
周波数解析
[ ここをクリックして展開 / 折りたたみ ]
高速フーリエ変換(FFT)を用いて、特定の周波数帯域のパワーを抽出する。
実数のFFTについてはnumpyのrfftで良い。 https://numpy.org/doc/stable/reference/generated/numpy.fft.rfft.html
その他、FFTに関するメソッドは下記を参照。 https://numpy.org/doc/stable/reference/routines.fft.html#module-numpy.fft https://docs.scipy.org/doc/scipy/reference/fft.html#
実装の流れ
- 人工データのパラメータ決定と定義 例: サンプル数(データ長)N, サンプリング周期dt, 信号周波数freq, ノイズ周波数noisefreqなどを定義する。
- 人工データの生成 例:
np.arangeで時間軸を生成し、np.sin(x)の$x$に使用して正弦波の時系列データを作成する。(設定した周波数freqに準拠させる)
その信号により高域の適当なノイズを付加したものを処理対象のデータとする。
""" 周波数解析 """
import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
if __name__ == "__main__":
# 10Hzのデータ、ノイズ40Hzの例, 自分でいろいろと試してみてください
ft = 10 # 基本周波数
ft_noise = 40 # ノイズ周波数
fs = 100 # サンプリング周波数
duration = 3 # 時間
dt = 1 / fs # Sampling period
t = np.arange(0, duration, step=dt)
N = len(t) # サンプル数
# 2つの周波数を持つ人工データの作成
signal_orgnl = # 自分で作成
signal_noise = # 自分で作成
signal_add = # 自分で作成, 信号とノイズを合成
# 周波数解析(numpyのrfftを使用)
spectrum =
# FFTの複素数結果を絶対値に変換
spectrum_abs =
# 周波数軸のデータ作成(x軸のメモリ)
fq = np.fft.rfftfreq(N, dt) # rfftを使った場合
# アルファ波を抽出
alpha_power =
# スペクトル表示
fig = plt.figure(figsize=(10, 5))
plt.xlabel("x軸のタイトル", fontsize=14) # xlabelの設定
plt.ylabel("y軸のタイトル", fontsize=14) # ylabelの設定
plt.plot( , , label="signal") # 周波数スペクトルのプロット
plt.tight_layout()
plt.show()
ローパスフィルタ(LPF)(参考)
[ ここをクリックして展開 / 折りたたみ ]
ローパスフィルタは特定の周波数帯域(遮断周波数 $f_c$ )以上の信号を除去するフィルタである。
ここでは、不要な帯域(ノイズ)を除去し、信号成分を明確にすることを目的とする。
下図はローパスフィルタの適用例である。 図右上の一番左の山(4Hz)が信号であり、その他の山を除去したいノイズとして10Hzの遮断周波数を設定している。
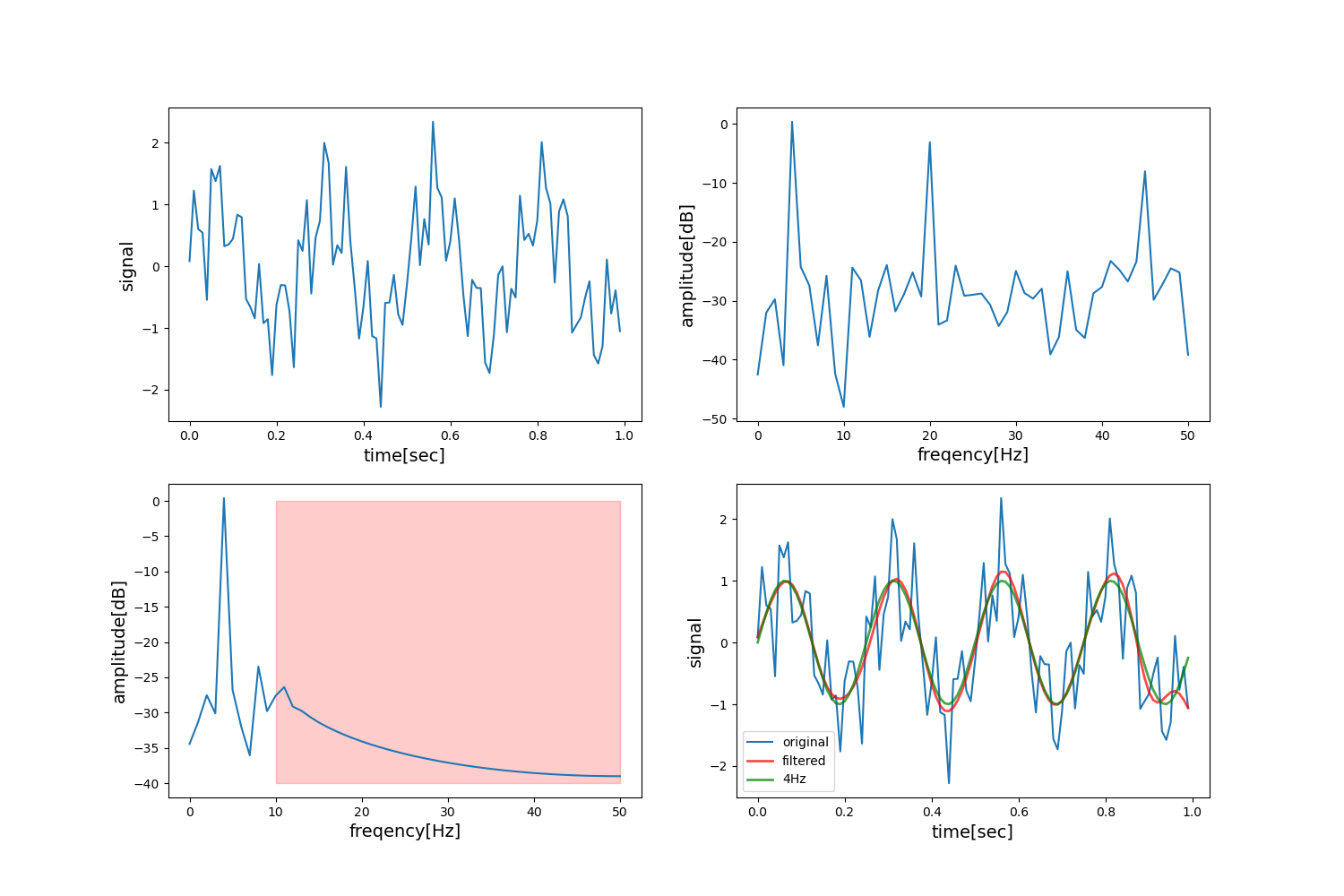
うまく適用できれば元の4Hzの成分を得ることができる。
実装の流れ
- パラメータの決定と定義 例: サンプル数(データ長)N, サンプリング周期dt, 信号周波数freq, ノイズ周波数noisefreqなどを定義する。
- 疑似データの生成 例:
- フィルタの適用 バタワースフィルタを作成し、信号にフィルタを適用する
np.arangeで時間軸を生成し、np.sin(x)の$x$に使用して正弦波の時系列データを作成する。(設定した周波数freqに準拠させる)
その信号により高域の適当なノイズを付加したものを処理対象のデータとする。
""" フィルタ処理 """
# バターワースフィルタ(バンドパス)
import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
def bandpass_butter_filt(sig, fs, fl, fh, N=4):
"""bandpass_butter_filt
Argument
---
sig -> ndarray : input signal
fs -> float : sampling frequency
fl -> float : lowcut frequency
fh -> float : highcut frequency
N -> int : order of filter
Return
---
ret -> ndarray : filtered signal with bandpass butterworth filter
"""
# (コーディング)
return ret
if __name__ == "__main__":
# 10Hzのデータ、ノイズ40Hzの例
ft = 10 # 基本周波数
ft_noise = 40 # ノイズ周波数
fs = 100 # サンプリング周波数
duration = 3 # 時間
# カットオフ周波数の定義
lowcut_f = 5 # [Hz]
highcut_f = 15 # [Hz]
dt = 1 / fs # Sampling period
t = np.arange(0, duration, step=dt)
N = len(t) # サンプル数
# 2つの周波数を持つ人工データの作成
signal_orgnl =
signal_noise =
signal_orgnl =
# フィルタリング処理
signal_filtered = bandpass_butter_filt(signal_orgnl, fs, lowcut_f, highcut_f)
# 周波数解析
spectrum_orgnl =
# FFTの複素数結果を絶対値に変換
spectrum_orgnl =
# 周波数軸のデータ作成
fq = np.fft.rfftfreq(N, dt)
# 周波数解析(フィルタ処理後)
spectrum_filtered =
spectrum_filtered =
# グラフ表示
# 時系列波形の比較
# フィルタ適用後のスペクトル
ダウンサンプリング(参考)
[ ここをクリックして展開 / 折りたたみ ]
大きすぎるサンプリング周波数はデータサイズを肥大化させ、各種処理が低速化してしまう。 そのためより低いサンプリング周波数になる様に信号を再サンプリングする事がある(ダウンサンプリング)。
元信号が持つ周波数成分を正確に再現するためには標本化定理(サンプリング定理)より以下の通り元信号が持つ最大の周波数成分$f$ [Hz]の2倍を超える周波数$f_s$ [Hz]によってサンプリングする必要がある。
\[fs > 2f\]例えば、遮断周波数$f_c$のローパスフィルタを通した信号が持つ最大の周波数成分はおよそ$f_c$となるため、再サンプリングに利用する周波数は$f_s > 2f_c$となる。ただし、ローパスフィルタの遮断周波数以降が瞬時に完全に減衰する事は無く遮断周波数以降の周波数成分が多少存在するために余裕を持たせる必要がある。
""" ダウンサンプリング """
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal
def generate_artific_signal(times):
"""適当な信号を生成"""
return ret
if __name__ == "__main__":
# Single trial
FS = 90 # サンプリング周波数
FS_DOWN = 30 # ダウンサンプル後の周波数
DURATION_S = 1 # 時間[s]
downsample_rate = int(np.ceil(FS / FS_DOWN))
n = int(np.floor(FS * DURATION_S)) # サンプル数
n_down = int(np.floor(FS_DOWN * DURATION_S)) # サンプル数(ダウンサンプリング後)
# 人工データの作成
t =
data = generate_artific_signal(t)
# 1. Resampling using scipy.siganal.resample
data_resample =
# 2. 自作ダウンサンプリング
t2 = np.arange(n_down) / FS_DOWN
# データを数個飛ばしに抽出
data_downsample =
# 3. decimation using scipy.signal.decimate
data_decimate =
# 図で確認
fig, ax = plt.subplots()
ax.set_title("downsampling")
ax.set_xlabel("Time [s]")
ax.set_ylabel("Amplitude [a.u.]")
ax.plot(t, data, label="oroginal")
ax.plot(t2, data_downsample, marker="o", label="downsample")
ax.plot(t2, data_resample, marker="s", label="resample")
ax.plot(t2, data_decimate, marker="D", label="decimate")
ax.legend()
plt.show()
加算平均(参考)
[ ここをクリックして展開 / 折りたたみ ]
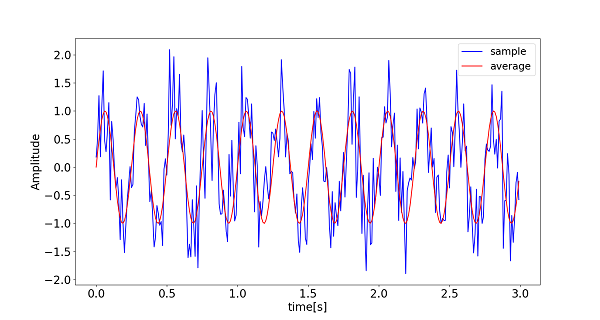
測定信号の位相が統一されている場合、それらを加算平均(足し合わせてその回数で割る)することでS/N比を改善することができる。
$N$回の加算平均を行うと、ノイズ成分は$1/\sqrt{N}$になることから、S/N比が$\sqrt{N}$倍改善することになる。
ただし、データの総数が減ることによるデメリットとのトレードオフとなるため、加算平均回数は重要なパラメータとなる。
実装の流れ
- 疑似データの生成 例: 適当な信号を作成し、ランダムノイズをかける。ループ処理で加算平均回数分作成する。
- 加算平均処理 作成したデータ同士を加算し、最後に加算回数で割る。 プロットしてノイズが低減したことを確認する。
トレンド補正(参考)
[ ここをクリックして展開 / 折りたたみ ]
生体信号に時間経過に応じて発生するトレンド成分を除去するための補正を実装する。 このトレンド(低周波成分)をベースラインと呼ぶ場合がある。ベースラインをどのように定義するかは一概には言えないが、最小二乗法により多項式近似した曲線をベースラインとして生成信号から減算する手法を取り上げる。
最小二乗法による $n$ 次の多項式近似においては、
\[\begin{aligned} y = a_{n}x^{n} + a_{n-1}x^{n-1} + \cdots + a_1x+a_0 \end{aligned}\]と元の信号の誤差の二乗和が最小となるように係数$a$の行列$A$を定める。
$N$次で近似するとき、
\[X = \begin{pmatrix} x_1^N & \cdots & x_1 & 1 \newline x_2^N & \cdots & x_2 & 1 \newline \vdots & \cdots & \vdots & \vdots \newline x_n^N & \cdots & x_n & 1 \end{pmatrix} , A = \begin{pmatrix} a_N \newline \vdots \newline a_0 \end{pmatrix} , Y = \begin{pmatrix} y_1 \newline \vdots \newline y_n \end{pmatrix}\]とおくと、係数行列Aは、
\[\begin{aligned} (X^TX)A = X^TY \end{aligned}\]より、
\[\begin{aligned} A = (X^TX)^{-1}X^TY \end{aligned}\]で求められる。
下図に疑似信号に対する処理の概要を示す。
今回は青線の信号に対して、紫線に示すような傾きとバイアスから構成される線形成分をベースライン(トレンド)として減算する処理を実装する。
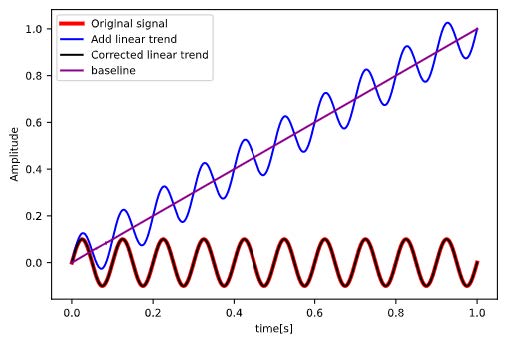
トレンド補正が正しく実装されていれば黒線で示されるように元の信号(赤線)と同様の結果が得られる。
実装の流れ
- 疑似データの生成 例:
- 最小二乗法による回帰直線の計算 $y = ax+b$の傾き$a$, 切片$b$を算出する。($S_{xy}: x,y$の共分散, $S_x^2: x$の分散, $\bar{x}・\bar{y}: $それぞれ$x・y$の平均) $$ \begin{aligned} a &=& \frac{S_{xy}}{S_x^2} \newline b &=& \bar{y} - a\bar{x} \end{aligned} $$
- トレンドを付加した信号から回帰直線を引いて元の信号に戻るか確認する
np.linespaceで時間軸を生成し、np.sin(x)の$x$に使用して正弦波の時系列データを作成する。
そこにトレンド成分を付加したものを補正対象の信号として用意する。(簡単なものなら$t$を足せば良い)